阅读以下说明和流程图,回答问题1至问题3。[说明]信息处理过程中经常需要将图片或汉字点阵做旋转处理。一个矩阵以顺时针方向旋转90°后可以形成另一个矩阵,如下图所示:流程图2-1描述了对n*n矩阵的某种处理。流程图2-2是将矩阵A顺时针旋转90°形成矩阵B的具体算法。请写出以下3*3单位矩阵沿顺时针方向旋转90°后所形成的矩阵。
题目
阅读以下说明和流程图,回答问题1至问题3。
[说明]
信息处理过程中经常需要将图片或汉字点阵做旋转处理。一个矩阵以顺时针方向旋转90°后可以形成另一个矩阵,如下图所示:
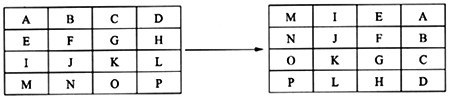
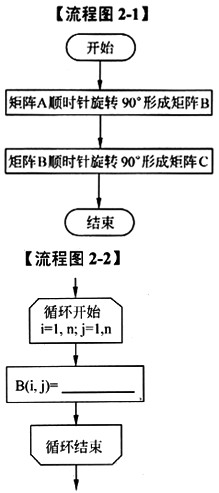
流程图2-1描述了对n*n矩阵的某种处理。流程图2-2是将矩阵A顺时针旋转90°形成矩阵B的具体算法。
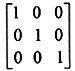
请写出以下3*3单位矩阵沿顺时针方向旋转90°后所形成的矩阵。
相似考题
更多“ 阅读以下说明和流程图,回答问题1至问题3。[说明]信息处理过程中经常需要将图片或汉字点阵做旋转处理。一个矩阵以顺时针方向旋转90°后可以形成另一个矩阵,如下图所示:流程图2-1描述了对n*n矩阵的某种处理。流程图”相关问题
-
第1题:
阅读以下说明和流程图将应填入(n)处的字句写在答题纸的对应栏内
【说明】
在一个矩阵中如果其零元素的个数远远多于其非零元素的个数时称这样的矩阵为稀疏矩阵稀疏矩阵通常采用三元组数组表示每个非零元素用一个三元组来表示即非零元素的行号列号和它的值然后按某种顺序将全部非零元素的三元组存于一个数组中例如对于以下二维数组

其中三元数组a的第行元素的值分别存储稀疏矩阵x的行数列数和非零元素的个数
下面的流程图描述了稀疏矩阵转换的过程
【流程图】

答案:

解析:
本题考查程序流程图及数组的操作

结合流程图中三个判断语句的结构和作用来分析第(5)空应该是i++它的作用是保证能取到稀疏矩阵中每一行的元素
-
第2题:
阅读以下说明和流程图,回答问题,并将解答填入对应栏内。
【说明】
求解约瑟夫环问题。算法分析:n个士兵围成一圈,给他们依次编号,班长指定从第w个士兵开始报数,报到第s个士兵出列,依次重复下去,直至所有士兵都出列。
【流程图】

【问题】
将流程图中的(1)~(5)处补充完整。
正确答案:(1)L[i].nextp=1 (2) k=w-1 (3) count!=n (4) ++I (5) ++count
(1)L[i].nextp=1 (2) k=w-1 (3) count!=n (4) ++I (5) ++count -
第3题:
试题一(共 20 分)阅读下列说明和图,回答问题 1 至问题 3,将解答填入答题纸的对应栏内。【说明】设有二维整数数组(矩阵)A[1:m,1:n],其每行元素从左至右是递增的,每列元素从上到下是递增的。以下流程图旨在该矩阵中需找与给定整数 X 相等的数。如果找不到则输出“false”;只要找到一个(可能有多个)就输出“True”以及该元素的下标 i 和 j(注意数组元素的下标从 1 开始)。例如,在如下矩阵中查找整数 8,则输出伟:True,4,12 4 6 94 5 9 106 7 10 128 9 11 13流程图中采用的算法如下:从矩阵的右上角元素开始,按照一定的路线逐个取元素与给定整数 X 进行比较(必要时向左走一步或向下走一步取下一个元素),直到找到相等的数或超出矩阵范围(找不到)。【流程图】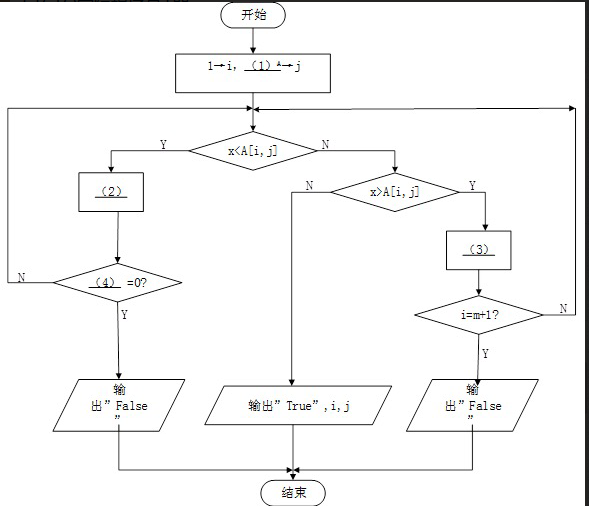
【问题】该算法的时间复杂数是()
供选择答案:A.O(1) B.O(m+n) C.(m*n) D,O(m2+n2)答案:解析:(1)n(2)j-1→j(3)i+1→I(4)j(5)C
【解析】
读题,可以看出元素查找的过程为从右上角开始,往右或者往下进行查找。因此,初始值i=1,j=n。如果查找值小于右上角值,则往右移动一位再进行比较。所以,第二空填j-1→j 。接下来是判断什么时候跳出循环。此时,终止循环的条件是:j=0,也就是其从最右端移到了最左端。再看X第4题:
阅读以下说明,回答问题,将解答填入对应的解答栏内。
. [说明] 请完成流程图以描述在数据A(1)至A(10)中求最大数和次大数的程序的算法。并将此改成PAD图。该算法的流程图如下图:
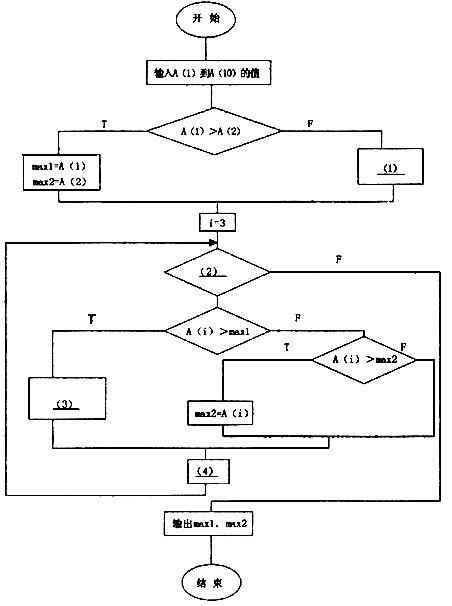 正确答案:(1)max2 =A(1) mex1 =A(2) (2)i< =10 (3)max1 =A(i)1 max2 = max1 (4)i=i+1
正确答案:(1)max2 =A(1) mex1 =A(2) (2)i< =10 (3)max1 =A(i)1 max2 = max1 (4)i=i+1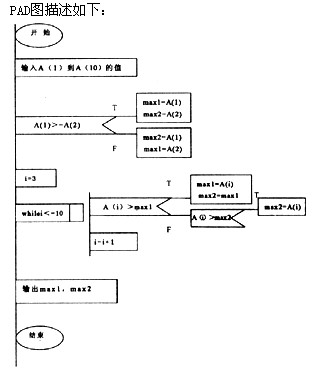
(1)max2 =A(1) mex1 =A(2) (2)i< =10 (3)max1 =A(i)1 max2 = max1 (4)i=i+1 解析:本题的算法思想是:先输入A(1)到A(10)的值,然后判断前两个数的大小。用变量max1存储最大数,用变量max2.存储次大数。然后逐个读入数据,分别和max1,max2比较,保证最大的存入max1,次大的存入max2。
解析:本题的算法思想是:先输入A(1)到A(10)的值,然后判断前两个数的大小。用变量max1存储最大数,用变量max2.存储次大数。然后逐个读入数据,分别和max1,max2比较,保证最大的存入max1,次大的存入max2。
第5题:
阅读下列说明和流程图,填补流程图中的空缺,将解答填入答题纸的对应栏内。 【说明】 设有二维整数数组(矩阵)A[1:m,1:n],其每行元素从左到右是递增的,每列元素从上到下是递增的。以下流程图旨在该矩阵中需找与给定整数X相等的数。如果找不到则输出“false”;只要找到一个(可能有多个)就输出“True”以及该元素的下标i和j(注意数组元素的下标从1开始)。 例如,在如下矩阵中查找整数8,则输出伟:True,4,1 2 4 6 9 4 5 9 10 6 7 10 12 8 9 11 13 流程图中采用的算法如下:从矩阵的右上角元素开始,按照一定的路线逐个取元素与给定整数X进行比较(必要时向左走一步或向下走一步取下一个元素),直到找到相等的数或超出矩阵范围(找不到)。
【流程图】
 【问题】该算法的时间复杂数是() 供选择答案:A.O(1) B.O(m+n) C.O(m*n) D,O(m²+n²)正确答案:(1)n
【问题】该算法的时间复杂数是() 供选择答案:A.O(1) B.O(m+n) C.O(m*n) D,O(m²+n²)正确答案:(1)n
(2)j-1→j
(3)i+1→I
(4)j
(5)C
